Сложные движения

Пpaктически все виды движений, которые совершает человек, состоят из поступательного и вращательного движений. Движения, при котором тело человека и его звенья участвуют одновременно в этих двух видах движения называется сложным.
К сложным относятся и другие виды движений, которые может совершать не только человек, но и спортивный снаряд, выпущенный им.
Поступательным называется движение, при котором любой отрезок, проведённый между произвольными точками внутри тела, не меняет своей ориентации относительно тела отсчёта. Траектории всех точек тела являются линиями, параллельными друг другу.
Вращательным является движение, при котором некоторое множество точек внутри тела остаются неподвижными относительно тела отсчёта и образуют ось вращения. Все остальные точки тела движутся относительно оси по концентрическим окружностям с одинаковой угловой скоростью.
Для измерения движения по окружности применяют следующие единицы измерения:
1) при измерении углов поворота радиус-вектора – градус (°).
2) при подсчёте оборотов вокруг оси: оборот (360°), пол-оборота (180°) и т. д.
3) для измерения угловой скорости во вращательных движениях – радиан. Радиан – угол, длина дуги которого равна радиусу окружности (рад = 57° 17\' 45")
Основной временной хаpaктеристикой вращательного движения является период (Т) – время полного оборота, совершаемого точками тела, измеряемого в секундах и других, кратных секунде единицах (минутах, часах и др.).
Частота вращения – это число полных периодов, укладывающихся на отрезке времени, равном единице, измеряемое в герцах (Гц).
Герц – единица частоты колебаний. Герц равен частоте такого колебания, период которого равен 1 с, то есть Гц равен одному циклу в 1 с.
Кроме временных параметров, вращательное движение хаpaктеризуется угловыми и линейными параметрами.
Основной хаpaктеристикой углового движения является угол поворота (φ), отсчитываемый от произвольно заданного уровня. Например, если нам необходимо подсчитать, на какой угол поворачивается тело прыгуна в воду с вышки, то за начальный можно выбрать угол между линией, проходящей через общий центр масс (ОЦМ) тела вдоль туловища в начальной позе, и вертикалью
Производными угловыми хаpaктеристиками являются: угловая скорость (ώ, рад /с), угловое ускорение (ε, рад /с ²).
Угловой скоростью тела называется отношение поворота радиус-вектора ко времени, за которое совершён поворот, рад /с:
,
где φ – угол поворота;
Угловым ускорением тела называется отношение изменения угловой скорости ко времени этого изменения, вычисленное в очень маленьком интервале данной точки траектории, рад /с ²:
Линейные хаpaктеристики описывают движение любой точки тела вдоль траектории, являющейся окружностью. К ним относятся:
• перемещение;
• путь;
• линейная скорость:
V = ώr,
где, r – радиус окружности;
• линейное ускорение, м /с ²:
а = εr
При вращении твёрдого тела относительно оси линейные скорости точек тела, лежащих на разных расстояниях от оси вращения различны, в то время, как угловая скорость всех его точек одинакова.
Поскольку точки тела движутся по криволинейным траекториям, существует нормальное ускорение, которое при движении по окружности называется центростремительным. Величина центростремительного ускорения определяется формулами:
Если скорость тела, движущегося по окружности, изменяется по величине, то наряду с центростремительным ускорением ацс будет иметь место и тангенциальное ускорение аtg.
Компоненты ускорения при неравномерном вращательном движении
В отличие от центростремительного ускорения, которое обусловлено изменением направления скорости, тангенциальное ускорение возникает из-за изменения вектора скорости:
Тангенциальное ускорение всегда направлено по касательной к окружности, и, если скорость увеличивается, его направление совпадает с направлением движения. Если же скорость уменьшается, то направление тангенциального ускорения противоположно вектору скорости. С тангенциальным ускорением мы встречаемся в спорте. Например, раскручивая молот, спортсмен сообщает ему тангенциальное ускорение для того, чтобы он приобрёл к моменту финального усилия максимально возможную скорость.
Раздел статьи: Биомеханика
Еще:
Спорт и здоровье -1 :: Спорт и здоровье -2 :: Спорт и здоровье -3 :: Спорт и здоровье -4 ::





 Ромашка повышает или понижает давление: как она влияет на его уровень у человека?
Ромашка повышает или понижает давление: как она влияет на его уровень у человека? Коричневые выделения при беременности: норма и патология
Коричневые выделения при беременности: норма и патология 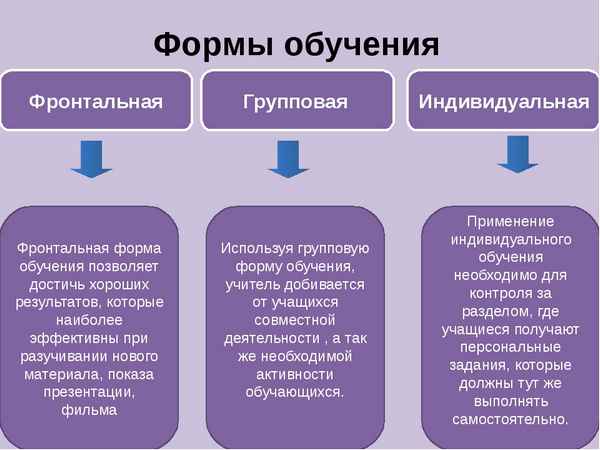 Формы обучения
Формы обучения  Гипотония и армия
Гипотония и армия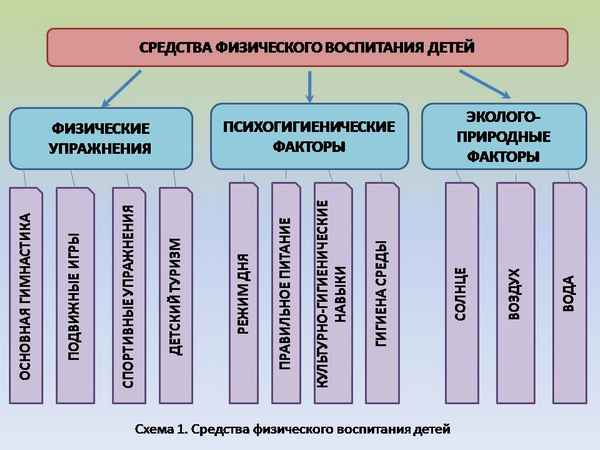 Вспомогательные средства физического воспитания детей школьного возраста
Вспомогательные средства физического воспитания детей школьного возраста  Как выглядят клопы, как их обнаружить?
Как выглядят клопы, как их обнаружить?  В окружении красных флажков
В окружении красных флажков